Today we’re going to look at how to filter items in tree data structures using Python 3. We’re going to compare a stateful approach and a functional and recursive approach. Finally, we discuss the advantages of a functional implementation.
The task
Assume we have a tree data structure in the form of nested lists, like the following
tree = ['root', [
['left_child', []],
['middle_child', [
['a leaf!', []]],
],
['right_child', [
['right_grandchild', [
['another leaf!']]]],
],
]
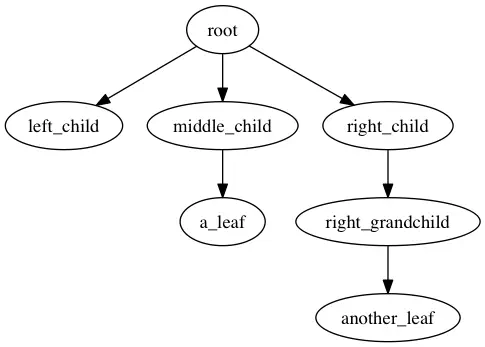
Tree diagram showing the tree data structure in the preceding listing
Find out path to all nodes that have the value Foobar. No constraints exist
for this tree, such as it being sorted. Thus, all nodes need to be inspected at
least once.
You can write this algorithm in many different ways. This post explores a few of these, and they all consist of these two parts:
- Code to visit all tree nodes
- Code to return a node if it matches
Foobar.
Before we can get started, we need to create some trees. I like creating
helpers, so a tree generator is going to be helpful. gen_tree recursively
creates a random tree with a depth of at most 3 layers.
def gen_tree(depth=0, max_depth=3):
return (
"Foobar" if randbool() else "Qux",
tuple(gen_tree(depth + 1) for _ in range(randint(0, 3)))
if depth < max_depth else tuple(),
)
If you want, you can include from random import seed; seed(1) in your code to
make sure that you get the same random tree for every execution. This can be
useful for debugging.
>>> pprint(gen_tree())
('Qux',
(('Foobar', (('Qux', (('Foobar', ()),)),)),
('Foobar', ()),
('Qux',
(('Qux', (('Qux', ()), ('Qux', ()), ('Foobar', ()))),
('Qux', (('Foobar', ()), ('Qux', ()), ('Qux', ()))),
('Foobar', (('Qux', ()), ('Qux', ()), ('Qux', ())))))))
Now, let’s see how we can find Foobar in this tree.
Stack-based traversal
If we’re going to traverse a tree structure, we need to take note of which nodes we’ve already visited and which we’ve not seen yet. If we traverse a tree in a predetermined order, for example depth-first in {pre,in,post}-order, we only need to be aware of which we need to visit in the future.
Wikipedia has useful illustrations showing the different kinds of tree traversals, so I won’t try to do a better job at it. Take a look right here.
def filter_tree(tree, keyword="Foobar"):
# Our first goal is the tree's root
# Additionally, we are going to store the path to the node
# As the second item in the tuple
goals = [(tree, [tree[0]])]
while goals:
node, path = goals.pop() # pop the first item in the goal queue
for child_node in node[1]:
# the path is the current path plus the turn taken
goals.append((child_node, path + [child_node[0]]))
if node[0] == keyword:
yield tuple(path)
I am going to be honest with you there. This code is messy and hard to debug.
We need to manually keep track of which paths in the tree need to be visited
and what the path to every node looks like. But it works. Here are all the
paths to nodes that have the value Foobar:
>>> pprint(tuple(filter_tree(tree)))
(('Qux', 'Qux', 'Foobar'),
('Qux', 'Qux', 'Qux', 'Foobar'),
('Qux', 'Qux', 'Qux', 'Foobar'),
('Qux', 'Foobar'),
('Qux', 'Foobar'),
('Qux', 'Foobar', 'Qux', 'Foobar'))
With yield, the caller can collect the individual results itself. That means
no result temporary list. In general, using yield statements makes code
more concise and is great for streaming data.
Instead of allocating memory for a full list, you can leverage yields paired
with other iterators to only need memory for the end result. This can be useful
if you nest list operations like
map(operator, filter(operator, reduce(operator, ...)))
It’s important to not forget to unpack an iterable stream once you want to
retrieve the results. Otherwise you are going to see a result like
<generator object <genexpr> at 0x...>.
Recursion-based traversal
Instead of explicitly tracking our current path and position in the tree, we can use a trick that functional programmers have figured out before it became cool: recursion.
In functional programming state often is encapsulated in the way functions are called. This has the neat advantage that if you call a function the same way twice, you get the same result. Not only does this make your code more predictable, it also helps writing saner tests with less dependency injection.
Let’s dive into the code
def filter_tree_recursive(tree, path=tuple(), keyword="Foobar"):
# Look ma, no assignment statements
if tree[0] == keyword:
yield (path + (tree[0], ))
for child_node in reversed(tree[1]):
yield from filter_tree_recursive(child_node, path + (tree[0], ))
Note the use of yield from, which is only available in Python 3. It lets us
delegate yield to another method. Otherwise we would have to unpack the
result of filter_tree_recursive into individual yields. This way, we can
shave off one line of code.
What our code does is return the path to the current node if it matches the search keyword plus call itself on all child nodes. Using the yield statement, we can avoid storing results in temporary variables. This makes the function itself store the state of execution. This can have side-effects, but not in our case.
Our code always fully evaluates the function and doesn’t suspend execution
since we’re constructing a tuple out of all yield results, as you can see
below. That means that once we’re done calculating, the Python runtime discards
the execution state of the current filter_tree_recursive call.
>>> pprint(tuple(filter_tree_recursive(tree)))
(('Qux', 'Qux', 'Foobar'),
('Qux', 'Qux', 'Qux', 'Foobar'),
('Qux', 'Qux', 'Qux', 'Foobar'),
('Qux', 'Foobar'),
('Qux', 'Foobar'),
('Qux', 'Foobar', 'Qux', 'Foobar'))
The result is the same, but our code is more predictable and testable.