Hack The Box challenges
Here are my writeups for retired Hack The Box challenges (this link requires logging in).
Hack The Box Marshal In The Middle Writeup
This article contains a writeup for the retired Hack The Box Marshal In The Middle challenge.
- Hack The Box Challenge page: https://app.hackthebox.com/challenges/27
- Time required: 30 min
The challenge has the following instructions:
The security team was alerted to suspicous network activity from a production web server.
Can you determine if any data was stolen and what it was?
Unpacking the archive
First, I check if I have the correct archive:
sha256sum "challenges/marshal_in_the_middle/Marshal in the Middle.zip"
I compare the checksum to the one given by Hack The Box, and it looks correct.
cdf53bab266ab4b8a28b943516bc064e9f966dae0a33503648694e15cb50ae2b challenges/marshal_in_the_middle/Marshal in the Middle.zip
I proceed by unpacking the archive:
unzip -P hackthebox \
"challenges/marshal_in_the_middle/Marshal in the Middle.zip" \
-d challenges/marshal_in_the_middle/ar/
This archive contains a packet capture file called chalcap.pcapng.
Archive: challenges/marshal_in_the_middle/Marshal in the Middle.zip
inflating: challenges/marshal_in_the_middle/ar/bro/conn.log
[...]
inflating: challenges/marshal_in_the_middle/ar/secrets.log
Deciphering the TLS conversations
I open chalcap.pcapng in Wireshark:
The packet dump chalcap.pcapng contains 13641 packets
Open in new tab
(full image size 297 KiB)
I try to decipher the individual TLS connections using bundle.pem. I also
need to tell Wireshark where it can find the key log secrets.log.
Learn more about how to decipher TLS traffic in Wireshark here.
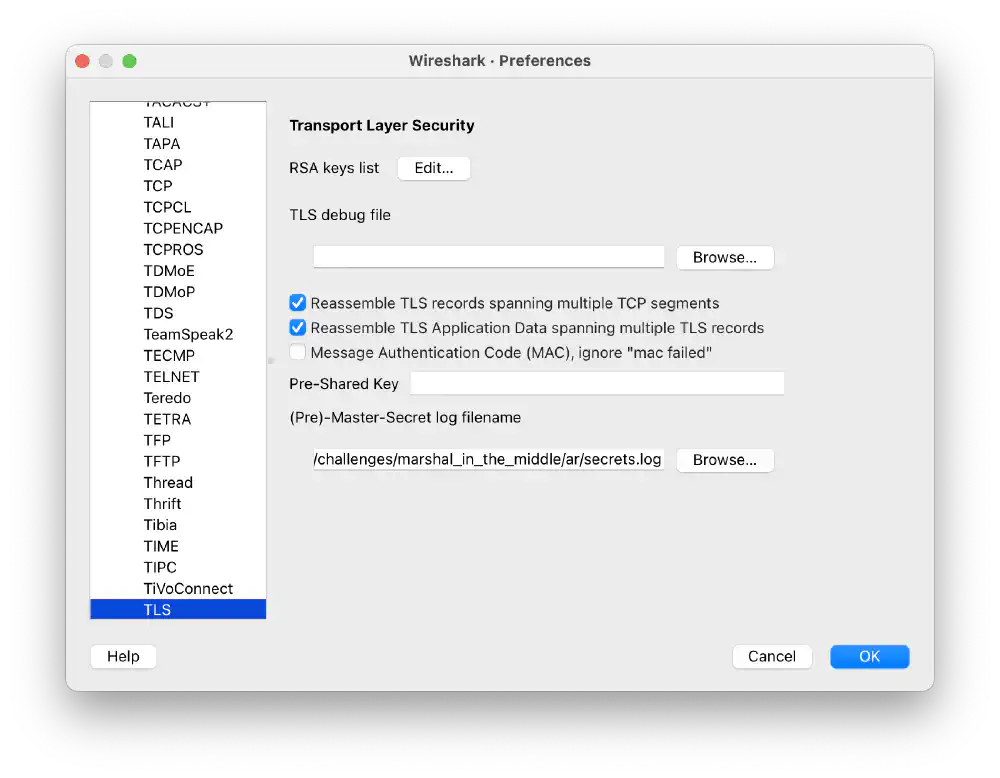
Screenshot of bundle.pem and secrets.log added to Wireshark
Open in new tab
(full image size 79 KiB)
Analyze individual conversations
I have deciphered all TLS conversations in the packet capture. I can now proceed in two different ways:
- Keep analyzing all connections by stripping away L1-L6 protocol headers. Work directly with L7 HTTP conversations
- Export all objects as retrieved through HTTP conversations
Stripping protocol headers
Use the “Export PDUs to File…” to strip away all L1-L6 information. Here, you can filter packets by HTTP, HTTP 2, and HTTP 3:
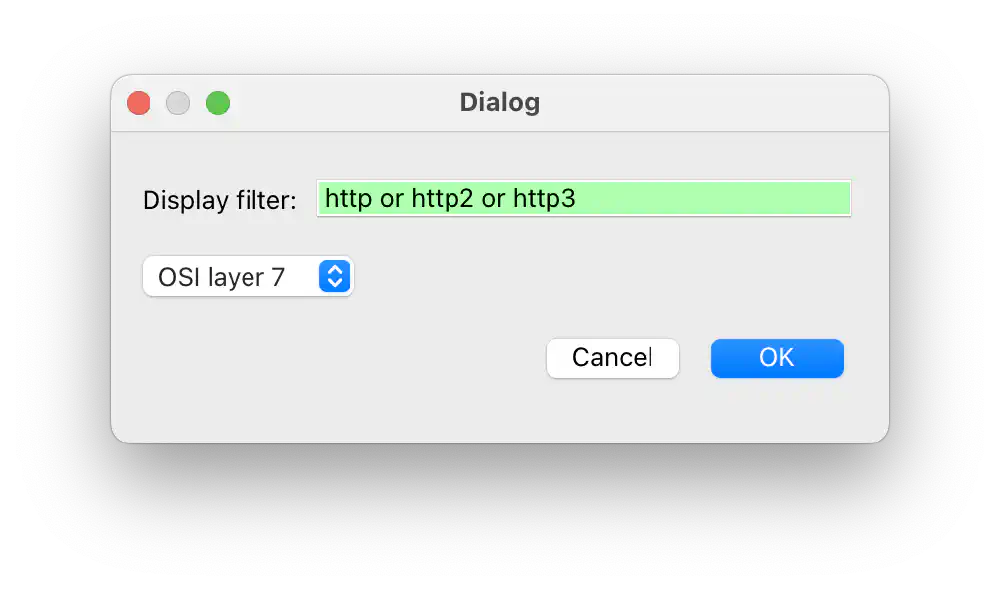
Exporting packet contents Open in new tab (full image size 39 KiB)
In a new Wireshark window, I see all HTTP conversations without their lower-layer protocol data:

All L7 HTTP/2/3 conversations exported Open in new tab (full image size 258 KiB)
Here, you can filter by http.file_data contains "HTB" to show packets
containing the flag. Inspecting the packet contents manually then reveals the
flag.
Exporting HTTP objects
Wireshark can export all HTTP bodies directly with the “Export Objects” dialog:
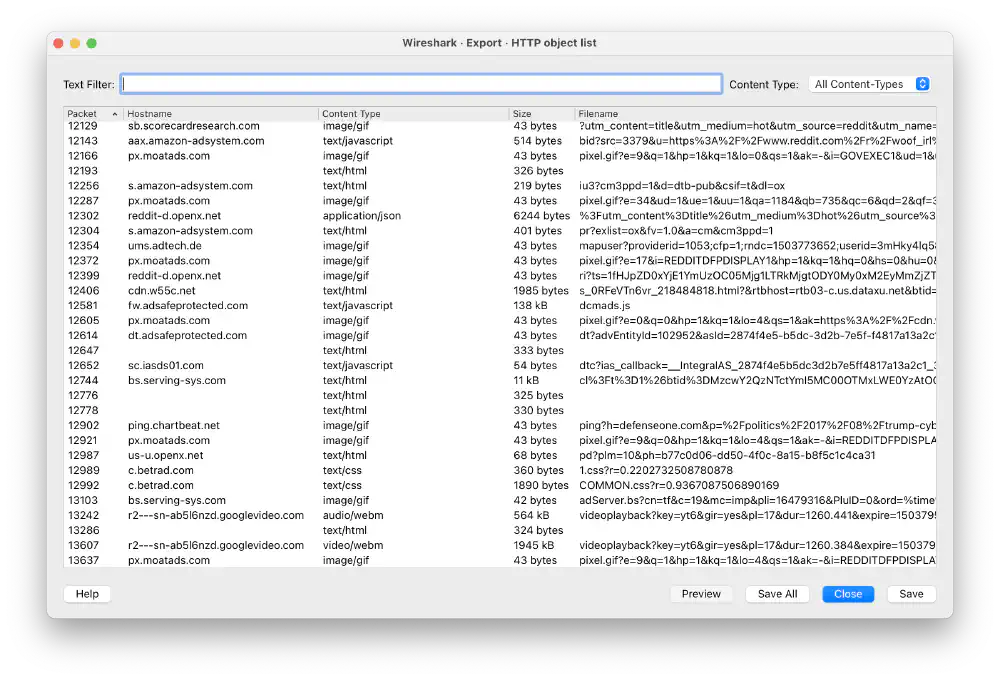
Exporting objects instead of PDUs Open in new tab (full image size 269 KiB)
I click “Save All” and store the HTTP objects in a new folder.
Grepping for the flag
Wireshark dumped all HTTP objects in a new folder. I can now search for the
flag by grepping for HTB:
grep -e "HTB" -r challenges/marshal_in_the_middle/http_objects/
grep immediately finds the flag:
challenges/marshal_in_the_middle/http_objects/api_post(4).php:HTB{...}
The file api_post(4).php contains a long array of American Express credit
card numbers. It appears that someone is stealing them. Better call the bank.
1 4m h4ckerm4n Open in new tab (full image size 63 KiB)
AAAAAAAAND, this again proves why forward secrecy is useful: it helps prevent exposure of confidential communications over HTTPS in case an attacker leaks key material. .
Hack The Box Weak RSA Writeup
This article contains a writeup for the retired Hack The Box Weak RSA challenge.
- Hack The Box Challenge page
- Time required: 1 h
- Date solved: 2024-09-02
The challenge contains these instructions:
Can you decrypt the message and get the flag?
Unpacking the challenge archive file
Unpack the challenge archive file using unzip:
unzip -P hackthebox challenges/weak_rsa/"Weak RSA.zip" \
-d challenges/weak_rsa
The archive contains two files:
inflating: challenges/weak_rsa/flag.enc
inflating: challenges/weak_rsa/key.pub
Decoding the public key
The file key.pub looks like a RSA public key. You can print the contents in
text form using openssl rsa -text:
openssl rsa -pubin -in challenges/weak_rsa/key.pub -text -noout
RSA public keys contain two large integers: modulus and exponent.
RSA Public-Key: (1026 bit)
Modulus:
03:30:3b:79:0f:b1:49:da:34:06:d4:95:ab:9b:9f:
b8:a9:e2:93:44:5e:3b:d4:3b:18:ef:2f:05:21:b7:
26:eb:e8:d8:38:ba:77:4b:b5:24:0f:08:f7:fb:ca:
0a:14:2a:1d:4a:61:ea:97:32:94:e6:84:a8:d1:a2:
cd:f1:8a:84:f2:db:70:99:b8:e9:77:58:8b:0b:89:
12:92:55:8c:aa:05:cf:5d:f2:bc:63:34:c5:ee:50:
83:a2:34:ed:fc:79:a9:5c:47:8a:78:e3:37:c7:23:
ae:88:34:fb:8a:99:31:b7:45:03:ff:ea:9e:61:bf:
53:d8:71:69:84:ac:47:83:7b
Exponent:
61:17:c6:04:48:b1:39:45:1a:b5:b6:0b:62:57:a1:
2b:da:90:c0:96:0f:ad:1e:00:7d:16:d8:fa:43:aa:
5a:aa:38:50:fc:24:0e:54:14:ad:2b:a1:09:0e:8e:
12:d6:49:5b:bc:73:a0:cb:a5:62:50:42:55:c7:3e:
a3:fb:d3:6a:88:83:f8:31:da:8d:1b:9b:81:33:ac:
21:09:e2:06:28:e8:0c:7e:53:ba:ba:4c:e5:a1:42:
98:81:1e:70:b4:a2:31:3c:91:4a:2a:32:17:c0:2e:
95:1a:ae:e4:c9:eb:39:a3:f0:80:35:7b:53:3a:6c:
ca:95:17:cb:2b:95:bf:cd
Bonus round: you can use openssl asn to show the underlying raw
ASN.1 syntax:
openssl asn1parse -in challenges/weak_rsa/key.pub
This shows the preceding openssl rsa -text output structure in its original
ASN.1 form:
0:d=0 hl=4 l= 287 cons: SEQUENCE
4:d=1 hl=2 l= 13 cons: SEQUENCE
6:d=2 hl=2 l= 9 prim: OBJECT :rsaEncryption
17:d=2 hl=2 l= 0 prim: NULL
--- v contains modulus and exponent v ---
19:d=1 hl=4 l= 268 prim: BIT STRING
Deriving the private key
To solve this challenge, you need the private key that decrypts the
contents of the file flag.enc. The challenge creator encrypted the contents
of this file using the public key file key.pub.
To decrypt this file, you need to have a
private key that matches this public key.
Normally, a public key modulus doesn’t let you derive the matching private key. That’s what makes RSA so secure. Only the owner of the private key can know the contents of the private key.
What if someone chooses a weak RSA key pair and someone guesses the private key just by looking at the public key?
In RSA, to derive the
public key modulus,
you need to find two large primes. These two primes are commonly called p and
q. In weak RSA an attacker can factor the modulus without much effort. This
reveals the primes used to create the private key. With the private key leaked,
an attacker can decipher any message encrypted with this key.
Parse and print out the modulus and exponent as integers using this Python script:
import re
modulus_raw = """
03:30:3b:79:0f:b1:49:da:34:06:d4:95:ab:9b:9f:
b8:a9:e2:93:44:5e:3b:d4:3b:18:ef:2f:05:21:b7:
26:eb:e8:d8:38:ba:77:4b:b5:24:0f:08:f7:fb:ca:
0a:14:2a:1d:4a:61:ea:97:32:94:e6:84:a8:d1:a2:
cd:f1:8a:84:f2:db:70:99:b8:e9:77:58:8b:0b:89:
12:92:55:8c:aa:05:cf:5d:f2:bc:63:34:c5:ee:50:
83:a2:34:ed:fc:79:a9:5c:47:8a:78:e3:37:c7:23:
ae:88:34:fb:8a:99:31:b7:45:03:ff:ea:9e:61:bf:
53:d8:71:69:84:ac:47:83:7b
"""
exponent_raw = """
61:17:c6:04:48:b1:39:45:1a:b5:b6:0b:62:57:a1:
2b:da:90:c0:96:0f:ad:1e:00:7d:16:d8:fa:43:aa:
5a:aa:38:50:fc:24:0e:54:14:ad:2b:a1:09:0e:8e:
12:d6:49:5b:bc:73:a0:cb:a5:62:50:42:55:c7:3e:
a3:fb:d3:6a:88:83:f8:31:da:8d:1b:9b:81:33:ac:
21:09:e2:06:28:e8:0c:7e:53:ba:ba:4c:e5:a1:42:
98:81:1e:70:b4:a2:31:3c:91:4a:2a:32:17:c0:2e:
95:1a:ae:e4:c9:eb:39:a3:f0:80:35:7b:53:3a:6c:
ca:95:17:cb:2b:95:bf:cd
"""
def parse(s: str) -> int:
return int(re.sub(r"\s|:", "", s), 16)
modulus = parse(modulus_raw)
exponent = parse(exponent_raw)
print(f"Modulus n: {modulus}")
print()
print(f"Exponent e: {exponent}")
print()
Running this script prints the following:
Modulus n: 573177824579630911668469272712547865443556654086190104722795509756891670023259031275433509121481030331598569379383505928315495462888788593695945321417676298471525243254143375622365552296949413920679290535717172319562064308937342567483690486592868352763021360051776130919666984258847567032959931761686072492923
Exponent e: 68180928631284147212820507192605734632035524131139938618069575375591806315288775310503696874509130847529572462608728019290710149661300246138036579342079580434777344111245495187927881132138357958744974243365962204835089753987667395511682829391276714359582055290140617797814443530797154040685978229936907206605
print()
Factorize the modulus n using
dCode’s prime factor decomposition
and receive the following two prime numbers for p and q:
20423438101489158688419303567277343858734758547418158024698288475832952556286241362315755217906372987360487170945062468605428809604025093949866146482515539
28064707897434668850640509471577294090270496538072109622258544167653888581330848582140666982973481448008792075646342219560082338772652988896389532152684857
Multiply p and q and verify that the result equals the modulus:
>>> p = 20423438101489158688419303567277343858734758547418158024698288475832952556286241362315755217906372987360487170945062468605428809604025093949866146482515539
>>> q = 28064707897434668850640509471577294090270496538072109622258544167653888581330848582140666982973481448008792075646342219560082338772652988896389532152684857
>>> modulus = 573177824579630911668469272712547865443556654086190104722795509756891670023259031275433509121481030331598569379383505928315495462888788593695945321417676298471525243254143375622365552296949413920679290535717172319562064308937342567483690486592868352763021360051776130919666984258847567032959931761686072492923
>>> p * q == modulus
True
The product p * q matches the modulus, and the prime factors found here work
as private key parameters. To automatically create the full private key form
p and q, you may want to write a script.
Solver script
Here’s a Python script called solve.py that achieves this:
You need two external libraries to run solve.py:
- SymPy: Perform modular arithmetic
- Cryptography: Construct private key
from
pandq.
The following shows solve.py and includes the modulus and exponent parse code
written before:
#!/usr/bin/env python3
import sympy
import re
from cryptography.hazmat.primitives.asymmetric import rsa
from cryptography.hazmat.primitives import serialization
modulus_raw = """
03:30:3b:79:0f:b1:49:da:34:06:d4:95:ab:9b:9f:
b8:a9:e2:93:44:5e:3b:d4:3b:18:ef:2f:05:21:b7:
26:eb:e8:d8:38:ba:77:4b:b5:24:0f:08:f7:fb:ca:
0a:14:2a:1d:4a:61:ea:97:32:94:e6:84:a8:d1:a2:
cd:f1:8a:84:f2:db:70:99:b8:e9:77:58:8b:0b:89:
12:92:55:8c:aa:05:cf:5d:f2:bc:63:34:c5:ee:50:
83:a2:34:ed:fc:79:a9:5c:47:8a:78:e3:37:c7:23:
ae:88:34:fb:8a:99:31:b7:45:03:ff:ea:9e:61:bf:
53:d8:71:69:84:ac:47:83:7b
"""
exponent_raw = """
61:17:c6:04:48:b1:39:45:1a:b5:b6:0b:62:57:a1:
2b:da:90:c0:96:0f:ad:1e:00:7d:16:d8:fa:43:aa:
5a:aa:38:50:fc:24:0e:54:14:ad:2b:a1:09:0e:8e:
12:d6:49:5b:bc:73:a0:cb:a5:62:50:42:55:c7:3e:
a3:fb:d3:6a:88:83:f8:31:da:8d:1b:9b:81:33:ac:
21:09:e2:06:28:e8:0c:7e:53:ba:ba:4c:e5:a1:42:
98:81:1e:70:b4:a2:31:3c:91:4a:2a:32:17:c0:2e:
95:1a:ae:e4:c9:eb:39:a3:f0:80:35:7b:53:3a:6c:
ca:95:17:cb:2b:95:bf:cd
"""
# Calculated using https://www.dcode.fr/prime-factors-decomposition
p = 20423438101489158688419303567277343858734758547418158024698288475832952556286241362315755217906372987360487170945062468605428809604025093949866146482515539
q = 28064707897434668850640509471577294090270496538072109622258544167653888581330848582140666982973481448008792075646342219560082338772652988896389532152684857
def parse(s: str) -> int:
return int(re.sub(r"\s|:", "", s), 16)
def main() -> None:
modulus = parse(modulus_raw)
exponent = parse(exponent_raw)
print(f"Modulus n: {modulus}")
print()
print(f"Exponent e: {exponent}")
print()
print(f"p: {p}")
print()
print(f"q: {q}")
print()
print(f"p x q = n {p*q == modulus}")
print()
# See
# https://en.wikipedia.org/wiki/RSA_(cryptosystem)#Example
# for all the calculations needed
l = sympy.lcm(p - 1, q - 1)
print(f"lcm(p-1,q-1) = {l}")
print()
d = sympy.mod_inverse(exponent, l)
print(f"d = {d} (modular inverse of e mod l)")
print()
print(f"(e x d) mod l = {(exponent * d) % l}")
e1 = d % (p - 1)
e2 = d % (q - 1)
coeff = sympy.mod_inverse(q, p)
print(f"e1 = d mod (p - 1): {e1}")
print()
print(f"e2 = d mod (q - 1): {e2}")
print()
print(f"coeff = q^-1 mod p: {coeff}")
print()
# Turn the above numbers into a RSA public/private key
public_numbers = rsa.RSAPublicNumbers(exponent, modulus)
private_numbers = rsa.RSAPrivateNumbers(p, q, d, e1, e2, coeff, public_numbers)
key = private_numbers.private_key()
# Serialize as PEM
pem = key.private_bytes(
encoding=serialization.Encoding.PEM,
format=serialization.PrivateFormat.TraditionalOpenSSL,
encryption_algorithm=serialization.NoEncryption(),
)
print(pem.decode())
if __name__ == "__main__":
main()
The following shows the full transcript when running solve.py:
Modulus n: 573177824579630911668469272712547865443556654086190104722795509756891670023259031275433509121481030331598569379383505928315495462888788593695945321417676298471525243254143375622365552296949413920679290535717172319562064308937342567483690486592868352763021360051776130919666984258847567032959931761686072492923
Exponent e: 68180928631284147212820507192605734632035524131139938618069575375591806315288775310503696874509130847529572462608728019290710149661300246138036579342079580434777344111245495187927881132138357958744974243365962204835089753987667395511682829391276714359582055290140617797814443530797154040685978229936907206605
p: 20423438101489158688419303567277343858734758547418158024698288475832952556286241362315755217906372987360487170945062468605428809604025093949866146482515539
q: 28064707897434668850640509471577294090270496538072109622258544167653888581330848582140666982973481448008792075646342219560082338772652988896389532152684857
p x q = n True
lcm(p-1,q-1) = 286588912289815455834234636356273932721778327043095052361397754878445835011629515637716754560740515165799284689691752964157747731444394296847972660708838124991689622165157918281276256721155732457712102522724762681364710411048102475196873015085333736454292995386264769757489409373849595177438542753003718646264
d = 44217944188473654528518593968293401521897205851340809945591908757815783834933 (modular inverse of e mod l)
(e x d) mod l = 1
e1 = d mod (p - 1): 44217944188473654528518593968293401521897205851340809945591908757815783834933
e2 = d mod (q - 1): 44217944188473654528518593968293401521897205851340809945591908757815783834933
coeff = q^-1 mod p: 8781217382420125056977279621675132530968943825983942088213575138391548383855591457031861314522182482985697327312492611417101340787613910676384093391819422
-----BEGIN RSA PRIVATE KEY-----
MIICOQIBAAKBgQMwO3kPsUnaNAbUlaubn7ip4pNEXjvUOxjvLwUhtybr6Ng4undL
tSQPCPf7ygoUKh1KYeqXMpTmhKjRos3xioTy23CZuOl3WIsLiRKSVYyqBc9d8rxj
NMXuUIOiNO38ealcR4p44zfHI66INPuKmTG3RQP/6p5hv1PYcWmErEeDewKBgGEX
xgRIsTlFGrW2C2JXoSvakMCWD60eAH0W2PpDqlqqOFD8JA5UFK0roQkOjhLWSVu8
c6DLpWJQQlXHPqP702qIg/gx2o0bm4EzrCEJ4gYo6Ax+U7q6TOWhQpiBHnC0ojE8
kUoqMhfALpUaruTJ6zmj8IA1e1M6bMqVF8srlb/NAiBhwngxi+Cbie3YBogNzGJV
h10vAgw+i7cQqiiwEiPFNQJBAYXzr5r2KkHVjGcZNCLRAoXrzJjVhb7knZE5oEYo
nEI+h2gQSt1bavv3YVxhcisTVuNrlgQo58eGb4c9dtY2blMCQQIX2W9IbtJ26KzZ
C/5HPsVqgxWtuP5hN8OLf3ohhojr1NigJwc6o68dtKScaEQ5A33vmNpuWqKucecT
0HEVxuE5AiBhwngxi+Cbie3YBogNzGJVh10vAgw+i7cQqiiwEiPFNQIgYcJ4MYvg
m4nt2AaIDcxiVYddLwIMPou3EKoosBIjxTUCQQCnqbJMPEQHpg5lI6MQi8ixFRqo
+KwoBrwYfZlGEwZxdK2Ms0jgeta5jFFS11Fwk5+GyimnRzVcEbADJno/8BKe
-----END RSA PRIVATE KEY-----
Store the RSA private key you have just created in a file called
challenges/weak_rsa/key.
Deciphering the flag
Using openssl rsautl, you can now decrypt the flag using the private key.
openssl rsautl -decrypt \
-in challenges/weak_rsa/flag.enc \
-inkey challenges/weak_rsa/key
Huzzah. This is the flag:
HTB{XXXXXXXXXXXXXXXXXXXXX}
Problems related to weak primes in RSA happen often and here are a few interesting links:
- Common primes factors by
badkeys - Math Stack Exchange on why not to choose close primes
- Fermat Attack on RSA